A százalékszámítás titkai

Múlt héten a rutintalanság eredményének mondtam egy posztban, hogy az egyik közvélemény-kutató intézet olyan számsort tett ki a pártpreferenciák megoszlásáról, amiben az egész számra kerekített százalékok összege 97% (a laikusok által természetesnek tartott 100 helyett). Azért, tettem hozzá (helyesen, de kifejezett helyeslés nélkül), mert a rutinosak általában inkább hozzáadnak ilyenkor annyit a tartalmilag nem olyan lényeges százalékokhoz (pl. a nem válaszolók, vagy a nem tudommal válaszolók arányához, esetleg az „egyéb pártként” szereplő resztli gyakoriságához), hogy kijöjjön a 100, és ezért ne botránkozzanak meg és kezdjenek el hiteltelenségre gyanakodni a számtant csak az iskolában látott olvasók.

Egy ismert közvélemény-kutató roppant negatívan reagált posztomra a kommentekben. Erre reagálva megígértem neki, hogy kiszámolom annak valószínűségét, hogy – mit tesz isten – az ő intézetének mind a 15 idén megjelent pártpreferencia adatsorában 100%-ra jön ki a kerekített számok összege (az adott intézetre egyébként korábban nem volt ez jellemző, és elvileg nem lehetetlen, hogy az intézetet a nyilvánosságban képviselő ingerült főnök nem tudott arról, hogy táblázatkészítő kollégái új szokásokat vettek fel az idén).

A számolgatás – és egy másik kolléga építő kommentje – egyben annak átgondolására is ösztökélt, hogy vajon mi lehet a legjobb gyakorlat ebben a kérdésben (ötcentesem a poszt végén), és azt is megállapította, hogy egyáltalán nem elképzelhetetlen, hogy 97-re vagy 103-ra jöjjön ki a számok összege egy ilyen adatsorban. De négy pontos eltérésre a 100-tól a mostanában szokásos pártpreferencia-adatok mellett egyáltalán nem számíthatunk manapság Magyarországon: ha ilyet lát, bátran sikítson! A legfontosabb eredmény a számolgatásomnak pedig az, hogy természetes módon a pártpreferencia adatsorok kicsit kevesebb, mint felében jöhet ki a kerekített százalékok összege 100-ra (ha azok pár 0-2 százalékos pártra is adnak külön becslést). A nyilvánosságban megjelenő pártpreferencia számsorokban viszont inkább 80% körüli a 100 előfordulási valószínűsége az utóbbi években, ha az összes kutatók adatait nézem az itt megosztott gyűjtésem alapján. Tehát …

Számoljon a számítógép, annak van erre ideje

2025-ben az egyik rendszeresen publikáló intézet öt egymás után megjelent havi pártpreferencia-vizsgálatának három-három adatsorában (az összes megkérdezett, a “biztos szavazók”, és a “biztos szavazó pártválasztók” között is) mindig 100-ra jött ki az egész számra kerekített százalékok összege. Ez más kutatóintézeteknél is gyakran előfordul hazánkban, pedig csöppet sem természetes. Ugyanis, ha 100-nál több embernek kettőnél több válaszlehetőséget megengedő kérdést teszünk fel, akkor az egyes válaszok egész számra felkerekített százalékos gyakorisága sokszor nem adja ki a természetesnek tűnő 100-at. Egyszerű példa: 102 emberből 34 azt mondja, hogy Fradi, ugyanennyien meg azt, hogy Újpest, és megint 34-en azt, hogy egyik se. Kerekített százalékban mindhárom csoport aránya 33%, tehát a három szám összege 99.

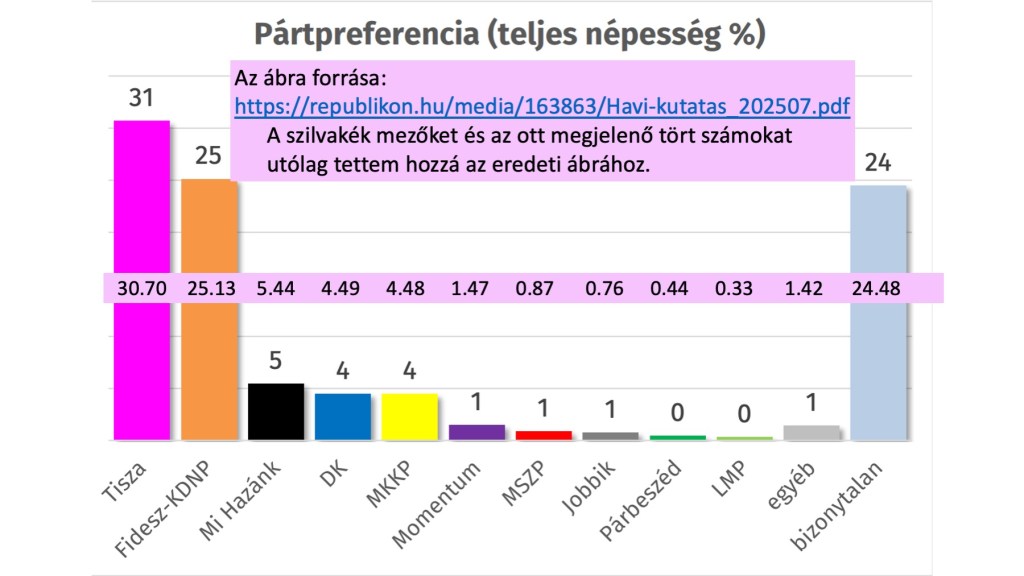
De (FRISS KIEGÉSZÍTÉS 2025. aug. 11-én) egy pixel-számlálásban jártas olvasóm segítségével a cikkem elején említett 97 összegű számsor mögötti kerekítetlen számokat is sikerült időközben kiböngészni, mivel az ábra, amiben eredetileg megjelentek a számok, szabad szemmel is láthatóan tört számokat tartalmaz. Hiszen a Párbeszéd nullája láthatólag magasabb oszlopként jelenik meg, mint az LMP-é, és a Momentum egyese is kimagaslik az MSZP és a Jobbik egyeséhez képest. Ezért megfelelő IT eszközökkel az ábra alapján ki lehet számolni a tört számokat, amelyek valójában meghatározták azt, hogy a közvélemény-kutató nyers adataiból milyen magasságú oszlopokat rajzolt az Excel (pixel-számlálásban jártas olvasóm segítségét ezúton is nagyon köszönöm). Két tizedesjegy pontosságú számokról van szó (beleírtam őket alább az eredeti ábrába, hogy lássák), és pont 100,0-ra jön ki az összegük.

Kezdő programozó is kiszámolhatja, hogy mennyire valószínű az, hogy 15 egymást követő számsorban a százalékok összege kerek százra jön ki, ha annyi válaszlehetőséget különböztetünk meg, mint ahányat az adott intézet szokott a pártpreferencia-vizsgálataiban, meg a százalékok is (hibahatáron belül) úgy alakulnak, mint az ő hathavi átlaguk 2025 első felében, és ráadásul még a „biztos szavazók” aránya meg a mintanagyság is úgy alakul, mint náluk szokott mostanában. Az általam használt kódot mindenki kipróbálhatja és újrafuttathatja, mert itt megosztom a megértéshez és használathoz szükséges magyarázatokkal (azért lehetőleg ne egy 1995-ből hátramaradt számítógépen használja, vagy ha mégis, akkor a “K=1000” sort semmi esetre se írja át “K=100000”-re, mint ahogy én tettem, mert százezres K esetén egy komolyabb hardveren is jó pár percet igényel majd a mulatság).

Egész konkrétan 100 ezer kísérletből egyszer se jött ki nekem az az eredmény, mint ami a szóban forgó kutatóintézetnek az idei év első felében. Öt hónap három-három számsora közül leggyakrabban 7-8-ban, tehát a 15 adatsor nagyjából felében fordulhat elő az ő pártpreferencia méréseikhez hasonló kutatásokban az, hogy pont 100 az egész számra kerekített százalékok összege. A százasok átlagos gyakorisága tizenöt adatsor között 7,3 körül alakult a százezer szimulációmban, elég nagy szóródással. Mindazonáltal annak, hogy 15 egymás után megjelenő számsor között 13 vagy több esetén jöjjön ki pont 100%-ra a kerekített százalékok összege, már egy százaléknál kisebbnek bizonyult a valószínűsége. A 15-nek meg lényegében semminek. Azaz annak előfordulásához már tényleg isteni közbelépés szükséges. Vagy mégse?

Mi lenne a helyes megoldás?

Mivel a matekos szimulációk tényleg egzaktak, ezért bízvást mondhatjuk, hogy vagy a Gondviselés kíméli meg a magyar nyilvánosságot attól, hogy jóval többször lásson nem 100%-ra összegződő számsorokat, vagy a kutatók végzik el inkább a Teremtő dolgát. Legalábbis a választási közvélemény-kutatások esetében, amiket eleve nagy gyanakvással szemlél a nagyérdemű. Én sokszor mutattam már rá arra, hogy tényleg nagy körültekintéssel kell olvasni őket. De az is kétségtelen, hogy velük kapcsolatban sokkal több annál az indokolatlan, de még a tájékozottabb olvasók közt is hitelt kapó vád, hogy a kutatóintézetektől józan ésszel elvárhassuk, hogy naivan várják be az ilyen kritikákat és az ezredik durva beszólás után is a kerekítési hibák halmozódásának számtani fogalmát magyarázgassák türelmesen a kommentelőknek. De mi mással próbálkozhatnak?

 A tudományban az a sztenderd megoldás – és jobb cégeknél ezt követik a komoly megrendelőknek leadott közvélemény-kutatási beszámolók is – hogy közlik a valós számokat, de lábjegyzetben odaírják, hogy a kerekítési hibák halmozódása miatt az összeg nem jön ki 100%-ra. Hát igen, de aki próbált már közvélemény-kutatást közölni a magyar nyilvánosságban, az tudja, hogy erre még az igényesebb nyomtatott lapokat is iszonyú nehéz rávenni. Az meg halálbiztos, hogy az online másodközlések akkor is elhagynák a lábjegyzetet, ha az eredeti forrásban még ott is lett volna. Ez az út itt tehát nem járható.

Ahogy az említett posztom alatt egy kiváló közvélemény-kutató rámutatott, az is egy megoldás, ha nem kerekítjük fel a számokat, hanem az első tizedesjegyre pontosan kiírjuk. (Ettől a probléma persze nem tűnik el, csak a 98 meg 101 helyett esetleg 99,9 és 100,2 lesz az összeg, amit viszont sokkal kevesebb olvasó fog észrevenni, főleg, akik a tizedesjegyet eleve nem értik.) Én mégse ajánlanám ezt a megoldást, mert ahogy a kolléga is írta, a tizedesjegy pontosságú számok közlése túlzott képzeteket keltene az olvasókban az adatok elvárható pontosságával kapcsolatban.

Harmadikként ott van az, hogy a politikailag kényes információktól távol álló, kevésbé lényeges százalékokba rejtik el a kerekítési hibát. Tudtommal ezt eredetileg még csak nem is a kutatók találták ki, hanem az igényesebb sajtónak a szemfüles, de a számtanban kihívásokkal küszködő olvasók által sokszór nem túl gyengéden megszólított munkatársai. Akárhonnan származzék is azonban az ötlet, eléggé elterjedt a hazai sajtóban.

Lennének persze sokkal csúnyább lehetőségek is, pl. hogy propagandacélokat követve csapják oda a kerekítési hibát egy, a szó szoros értelmében tetszés szerint kiválasztott párthoz vagy kategóriához.

A propagandacélokat követő adathamisítás nyilvánvalóan bűnös gyakorlat, ha előfordul (hogy előfordul-e, azt nem tudom megerősíteni, de cáfolni sem). A harmadikként említett megoldást viszont én a magam részéről megértéssel elfogadom, legalábis a választási közvélemény-kutatások szenzitív és sok csatát látó világában. Annyit talán lehetne javítani ezen a gyakorlaton is, hogy ilyenkor egyértelműen megmondják, hogy melyik válaszkategóriához csapták hozzá a kerekítési hibát. Mert azt talán még el lehetne adni a sajtónak, ha az ábrákban és táblákban pl. „nincs válasz” helyett „nincs válasz és kerekítési hiba” szerepelne.

A Vox Populi választási kalauz által követett gyakorlat egyébként az, hogy minden itt átlagolt-bemutatott számsort az ábráink és a számítások céljára átszámolok úgy, hogy a kerekítési hibát arányosan osztom el az összes válaszkategóriák közt (ennek módja az, hogy az eredetileg a sajtóban megjelent százalékokat elosztom azok összegének egy századával – ha az összeg 100, akkor az osztó 1, ha 101, akkor 1,01, ha 98, akkor 0.98 és így tovább). Viszont tizedesjegy pontosságú számokat inkább csak akkor mutatok meg számszerűen kinyomtatva, ha több számsor valamilyen átlagáról vagy egyéb képzett statisztikáról van szó. Ahol egész számokat említek, vagy ilyen jelenik meg táblázatokban, ott az eredetileg a közvélemény-kutatók által megjelentett számokról van szó. Saját közvélemény-kutatási beszámolókban pedig leginkább ott hagyom a kerekítési hibát a táblázatokba kerülő egész számokban (ld. pl. legutóbb itt).

(FRISS, 2025. 07. 18.) A Választási tudásbázis blog szerzője vetette fel, hogy az is megoldás lehetne, ha egy-egy szám helyett intervallumokat mutatnának be a közvélemény-kutatók táblái. A nyilvánvaló hátulütő az, hogy a laikusok számára ez még zavarosabb képet teremthetne. Szerintem azonban lenne egy ezért valamelyest kompenzáló plusz előnye is ennek a megoldásnak, ha hangsúlyozottan a hibahatárt jelölné az intervallum, tehát mondjuk Kutyapárt=4% helyett Kutyapárt: 3-5% kerülne adott esetben egy táblázatba. Ami lehet, hogy néhány laikust legyintésre késztetne (ugyan kit érdekel ez a számsor, ha ennyire bizonytalan a becslés), de lehet, hogy ez csak azt jelezné, hogy végre megértették, mit is jelent a hibahatár.

A poszt illusztrációját a Mover magazine “A számok, a szentségek és a jóslatok varázslata Hieronymus Bosch festményein” című cikkéből vettem át, és Jeroen Antonison van Aken „A földi élvezetek kertje” című oltárképének egy részletét ábrázolja a Prado gyűjteményéből.